Series temporales¶

Apuntes en construcción

Actualmente estos apuntes están en proceso de creación. Probablemente estén terminados para navidades del 2025.

Una serie temporal es un conjunto de valores que se miden y, por lo tanto, se almacenan de forma secuencial en el tiempo, de manera que el orden cronológico es fundamental.

Estos valores normalmente se miden en intervalos regulares de tiempo, de manera que están espaciados en el tiempo con la misma separación temporal, ya sean horas, minutos, días, meses, trimestres, etc... La forma más sencilla de comenzar el análisis de una serie temporal es mediante su representación gráfica. En el eje X (horizontal) se representa el tiempo, y en el eje Y (vertical), los valores a analizar:

Ejemplo de serie temporal - ingresos por acción

En IoT, cada sensor genera datos etiquetados con un timestamp (marca temporal).

Al capturar datos de series temporales a lo largo de un periodo determinado, podemos observar cómo ha evolucionado o cambiado el sistema, lo que ayuda a identificar tendencias, tomar medidas proactivas o hacer predicciones futuras. Por ejemplo, trabajamos con datos de series temporales cuando revisamos el uso de CPU y memoria de un servidor durante la última semana, exploramos las fluctuaciones del tipo de cambio de divisas durante los últimos tres meses o analizamos las constantes vitales de un paciente recogidas durante el último año.

Las series temporales se caracterizan por una generación regular (métrica) o irregular (evento) de periodos temporales. Además, implican grandes volúmenes de datos, como pueden ser ficheros de logs o sensórica de elementos IoT, los cuales tienen una alta frecuencia de creación.

Dadas estas características, las series temporales se emplean principalmente para la predicción y análisis de tendencias en muchos servicios financieros y aplicaciones IoT.

Características¶

Tendencia
Estacionalidad
Ciclo
Aleatoriedad

Toda serie temporal tiene dos características clave:

Cada punto de datos incluye la hora asociada a la medición o evento.
Los datos de series temporales son, por naturaleza, de tipo "append-only", lo que significa que una vez registrada y almacenada una medición o evento, nunca se actualiza.

Si nos centramos en las características de los datos provenientes de sensórica IoT, podemos destacar:

Dependencia temporal: los datos cercanos en el tiempo suelen estar correlacionados.
Tamaño creciente: en IoT, los datos llegan en flujo continuo (data stream).
Importancia del tiempo: el análisis depende tanto del valor como del momento.
Alta frecuencia de muestreo: Los sensores pueden generar datos a intervalos muy cortos (por ejemplo, cada milisegundo).
Variabilidad en la calidad de los datos: Los datos pueden verse afectados por interferencias, ruido o fallos en el sensor.

Un sensor de temperatura en un invernadero que registra:

timestamp	temperatura
2025-08-11 10:00:00	23.4
2025-08-11 10:00:01	23.5
2025-08-11 10:00:02	23.6

Componentes¶

Una serie temporal puede descomponerse en:

Componente	Descripción	Ejemplo
Tendencia (Trend)	Cambio a largo plazo	Aumento progresivo de temperatura media en 5 años
Estacionalidad (Seasonality)	Patrón que se repite de forma periódica	Pico de tráfico en una red cada día a las 20:00
Ciclo (Cycle)	Fluctuaciones no regulares pero de cierta periodicidad	Ciclos de carga de una batería en uso
Ruido (Noise)	Variación aleatoria sin patrón	Lecturas erráticas por interferencia electromagnética

Visualización con Python:

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from statsmodels.tsa.seasonal import seasonal_decompose

# Simulación de datos
rng = pd.date_range('2025-01-01', periods=100, freq='H')
trend = np.linspace(20, 25, 100)
seasonal = 2 * np.sin(np.linspace(0, 6*np.pi, 100))
noise = np.random.normal(0, 0.5, 100)
data = trend + seasonal + noise

ts = pd.Series(data, index=rng)
decomp = seasonal_decompose(ts, model='additive', period=24)
decomp.plot()
plt.show()

Series temporales en IoT

Volumen y velocidad:
- Sensores pueden enviar miles de mediciones por segundo.
- Necesario procesar en streaming (Kafka, Flink, Spark Streaming).
Datos faltantes:
- Causados por pérdida de señal o fallos de hardware.
- Estrategias: interpolación, forward-fill, estimación con modelos.
Valores atípicos (outliers):
- Pueden ser fallos o eventos reales.
- Necesario definir umbrales y métodos de detección.
Multicanalidad:
- Ej. estación meteorológica con temperatura, humedad y presión.
Sincronización:
- Ajustar todos los datos a UTC y compensar desincronización de relojes.

Almacenamiento¶

Tipo	Ejemplos	Ventajas	Inconvenientes
TSDB (Time Series DB)	InfluxDB, TimescaleDB, QuestDB	Optimización por tiempo, retención, compresión	Necesidad de aprender consultas específicas
NoSQL	MongoDB, Cassandra	Escalabilidad horizontal	Menos funciones específicas para series temporales
SQL + extensiones	PostgreSQL + Timescale	Integración con SQL, potente indexado	Rendimiento menor que TSDB puras en casos masivos

Ejemplo: consulta en InfluxQL

SELECT MEAN(temperature) FROM sensor_data
WHERE time >= now() - 1h
GROUP BY time(1m)

Herramientas

Herramientas y Entornos de Trabajo

Python: pandas, numpy, statsmodels, scikit-learn, prophet.
Streaming: Kafka, Flink, Spark Streaming.
Visualización: Grafana, Plotly, Matplotlib.

Uso de Pandas¶

A la hora de trabajar con datos que contienen series temporales en Pandas, la clave reside en que el índice del DataFrame sea de tipo DatetimeIndex.

La forma más común de lograr esto es asegurarse de que la columna que contiene las fechas esté en el formato correcto y luego establecerla como índice.

Para ello, podemos utilizar las siguientes funciones de Pandas:

pd.to_datetime: convierte una Serie o un valor en un valor timestamp, infiriendo el formato recorriendo toda los datos de la Serie
pd.to_timedelta: convierte una Serie en una diferencia absoluta de tiempo
pd.date_range(): permite generar secuencias de fechas/tiempos

Vamos a realizar un ejemplo sencillo, con los datos del Ibex35 extraídos de Yahoo Finance.

El primer paso es cargar el DataFrame y ver su estructura

import pandas as pd

ibex = pd.read_csv("ibex35_2020_2025.csv")

Si comprobamos su contenido, vemos que tenemos un campo Date con la fecha de cada valor:

ibex.head()
#    Date        Close        High         Low          Open         Volume
# 0  2020-01-02  9691.200195  9705.400391  9615.099609  9639.099609  142379600
# 1  2020-01-03  9646.599609  9650.700195  9581.200195  9631.200195  135130000
# 2  2020-01-06  9600.900391  9618.200195  9492.700195  9585.400391  103520400
# 3  2020-01-07  9579.799805  9657.900391  9557.900391  9623.099609  133476100
# 4  2020-01-08  9591.400391  9604.299805  9520.299805  9535.099609  133957600

Para asegurarnos de que la columna Date se interprete correctamente como un índice de tipo DatetimeIndex, podemos utilizar la función pd.to_datetime() para convertirla antes de establecerla como índice.

ibex['Date'] = pd.to_datetime(ibex['Date'])
ibex.set_index('Date', inplace=True)

Otra forma más rápida es cargar directamente el CSV indicando qué columna queremos utilizar como indice:

ibex = pd.read_csv("ibex35_2020_2025.csv", parse_dates=["Date"], index_col="Date")

En ambos casos, obtenemos un DataFrame con la siguiente información:

ibex.head()
#             Close        High        Low           Open         Volume
# Date                                                                     
# 2020-01-02  9691.200195  9705.400391  9615.099609  9639.099609  142379600
# 2020-01-03  9646.599609  9650.700195  9581.200195  9631.200195  135130000
# 2020-01-06  9600.900391  9618.200195  9492.700195  9585.400391  103520400
# 2020-01-07  9579.799805  9657.900391  9557.900391  9623.099609  133476100
# 2020-01-08  9591.400391  9604.299805  9520.299805  9535.099609  133957600

Operaciones¶

Una vez tenemos el DataFrame con el índice de tipo DatetimeIndex, podemos realizar diversas operaciones y análisis sobre la serie temporal.

Por ejemplo, podemos filtrar los datos con un valor concreto o utilizando subconjuntos de la propia fecha:

# Un valor concreto
ibex250602 = ibex.loc['2025-06-02']
# Todos los valores de un mes
ibex2506 = ibex.loc['2025-06']
# Todos los valores de un año
ibex25 = ibex.loc['2025']

Una vez tenemos un conjunto de datos, podemos obtener información sobre los índices accediendo a la propiedad index y a partir de ahí, a sus propiedades month, year, is_quarter_end, etc...

Por ejemplo, si partimos del DataFrame con los valores de año 2025:

ibex25.index.month, ibex25.index.year
# (Index([1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
#         ...
#         7, 8, 8, 8, 8, 8, 8, 8, 8, 8],
#        dtype='int32', name='Date', length=157),
#  Index([2025, 2025, 2025, 2025, 2025, 2025, 2025, 2025, 2025, 2025,
#         ...
#         2025, 2025, 2025, 2025, 2025, 2025, 2025, 2025, 2025, 2025],
#        dtype='int32', name='Date', length=157))

Un caso particular es is_quarter_end, el cual devolverá una lista con True en aquellos días que son el último día de un trimestre. Si lo usamos para localizar dichos elementos, el resultado son los días finales de cada trimestre, independientemente de si es el 30 o el 31 del mes en cuestión:

ibex25.loc[ibex25.index.is_quarter_end]
#             Close         High          Low           Open          Volume
# Date                                                                         
# 2025-03-31  13135.400391  13249.799805  13051.799805  13224.599609  167060300
# 2025-06-30  13991.900391  14029.099609  13894.400391  14025.599609  110470200

También podemos seleccionar un subconjunto por un rango temporal:

ibex24 = ibex['2024-01-01 00:00':'2025-01-01 00:00']
ibex24.shape
# (256, 5)

La operación de resampling (utilizando la función resample) permite cambiar la frecuencia de los datos temporales, ya sea aumentando o disminuyendo la granularidad a días (D), meses (M), trimestres (Q), años (A), etc...

El remuestreo es similar a una consulta group by, salvo que en lugar de producir un resultado por valor de una columna, obtenemos un resultado por fragmento temporal, empezando por el punto más antiguo y terminando por el más reciente.

Por ejemplo, podemos obtener la media mensual de los datos (fíjate que el índice ha tomado como valor el último día de cada mes):

media_mensual = ibex24.resample('M').mean()
media_mensual.head()
#             Close          High           Low         Open          Volume
# Date                                                                     
# 2024-01-31  10016.259011  10069.972701   9957.822665  10020.490945  1.312984e+08
# 2024-02-29  10003.104771  10053.933315   9961.880999  10014.028506  1.414177e+08
# 2024-03-31  10571.425049  10605.965039  10504.600000  10521.364941  1.776267e+08
# 2024-04-30  10870.609561  10942.638021  10807.738281  10880.161877  1.746393e+08
# 2024-05-31  11199.186346  11236.586337  11134.386364  11178.250044  1.707392e+08

Tras el resampling, podemos realizar las agregaciones que queramos con la función agg():

media_mensual.agg(['mean', 'min', 'max'])
#       Close         High          Low           Open          Volume
# mean  11044.879507  11099.089394  10982.163324  11039.518731  1.316156e+08
# min   10003.104771  10053.933315   9957.822665  10014.028506  9.708670e+07
# max   11783.330460  11838.421748  11717.534774  11784.673998  1.776267e+08

Otras operación que podemos realizar es desplazarnos sobre los datos utilizando la operación shift, pudiendo simular las funciones ventana lag y lead (anterior y siguiente). Por ejemplo, para crear dos columnas con los valores de cierre anteriores y posteriores, podemos hacer:

media_mensual['Close_lag'] = media_mensual['Close'].shift(1)
media_mensual['Close_lead'] = media_mensual['Close'].shift(-1)
media_mensual.head()

#             Close         High          Low           Open         Volume         Close_lag     Close_lead 
# Date                                                                 
# 2024-01-31  10016.259011  10069.972701   9957.822665  10020.490945  1.312984e+08           NaN  10003.104771  
# 2024-02-29  10003.104771  10053.933315   9961.880999  10014.028506  1.414177e+08  10016.259011  10571.425049  
# 2024-03-31  10571.425049  10605.965039  10504.600000  10521.364941  1.776267e+08  10003.104771  10870.609561  
# 2024-04-30  10870.609561  10942.638021  10807.738281  10880.161877  1.746393e+08  10571.425049  11199.186346  
# 2024-05-31  11199.186346  11236.586337  11134.386364  11178.250044  1.707392e+08  10870.609561  11160.760059

Mediante la función rolling podemos calcular estadísticas móviles sobre la serie temporal. Por ejemplo, para calcular la media móvil de los últimos 5 períodos:

media_movil = media_mensual.rolling(window=5).mean()
media_movil.head()

#             Close          High           Low          Open        Volume     Close_lag    Close_lead 
# Date                                                                 
# 2024-01-31           NaN           NaN           NaN           NaN           NaN           NaN           NaN  
# 2024-02-29           NaN           NaN           NaN           NaN           NaN           NaN           NaN  
# 2024-03-31  10196.929610  10243.290351  10141.434555  10185.294797  1.501143e+08           NaN  10481.713127  
# 2024-04-30  10481.713127  10534.178792  10424.739760  10471.851775  1.645612e+08  10196.929610  10880.406985  
# 2024-05-31  10880.406985  10928.396466  10815.574882  10859.925621  1.743351e+08  10481.713127  11076.851988

Finalmente, podemos realizar una interpolación de los datos utilizando la función interpolate para rellenar los valores nulos:

media_filled = media_mensual.interpolate(method="linear", limit_direction='both')
media_filled.head(3)

#             Close         High          Low           Open         Volume         Close_lag     Close_lead 
# Date                                                                 
# 2024-01-31  10016.259011  10069.972701   9957.822665  10020.490945  1.312984e+08  10016.259011  10003.104771  
# 2024-02-29  10003.104771  10053.933315   9961.880999  10014.028506  1.414177e+08  10016.259011  10571.425049  
# 2024-03-31  10571.425049  10605.965039  10504.600000  10521.364941  1.776267e+08  10003.104771  10870.609561

Modelos estadísticos¶

ARIMA / SARIMA: para predicciones cuando hay autocorrelación.
Holt-Winters: suavizado exponencial con tendencia y estacionalidad.

Ejemplo ARIMA:

from statsmodels.tsa.arima.model import ARIMA

model = ARIMA(ts, order=(2,1,2))
model_fit = model.fit()
forecast = model_fit.forecast(steps=10)
print(forecast)

Ejecutando métricas de valores¶

Análisis de Fourier¶

Correlación¶

Random Walks¶

Modelos ARIMA¶

https://cienciadedatos.net/documentos/py51-modelos-arima-sarimax-python

Modelos ARCH¶

Uso de ML¶

Machine Learning¶

LSTM / GRU para dependencias largas.
Modelos de regresión con variables temporales.

Detección de anomalías¶

# Umbral simple
threshold = ts.mean() + 3*ts.std()
anomalies = ts[ts > threshold]

Buenas Prácticas¶

Usar timestamp en UTC.
Documentar frecuencia y precisión de cada sensor.
Implementar pipelines de limpieza.
Establecer políticas de retención.
Validar la calidad de datos en streaming.

Sus valores pueden ser:

discretos: entre un conjunto finito de valores, por ejemplo, la cantidad de hermanos en una familia. Se suelen expresar mediante un número entero.
continuos: tienen un cantidad infinita de valores y se expresan mediante número reales, por ejemplo, la temperatura que recoge un sensor.

Estacionalidad y comportamiento de tendencia¶

Toda serie temporal se puede dividir en tres componentes:

Tendencia (Trend), cuando el crecimiento o su decrecimiento es constante conforme avanza el tiempo, y representa el cambio a largo plazo de la serie.
Estacionalidad (Seasonal), cuando la serie se repite en patrones periódicos a modo de temporadas, representando fluctuaciones que se repiten en periodos fijos.
Residual / Remanente (Residuals), son aquellas irregularidades o ruido que no son explicables por la tendencia ni la estacionalidad.

Visualizar por separado estos tres componentes de una serie temporal se conoce como descomposición:

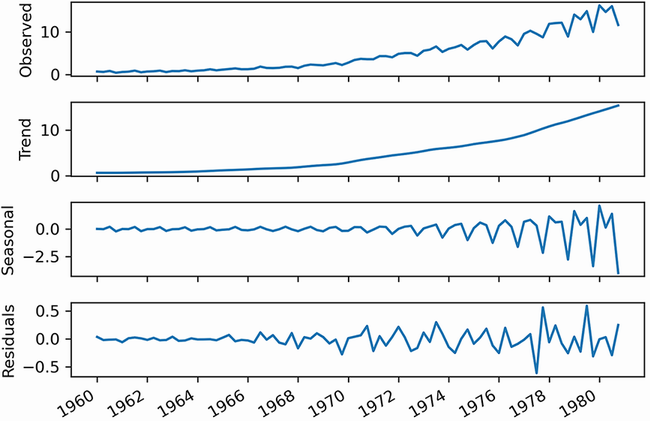
Descomposición de serie temporal - ingresos por acción

Si analizamos cada gráfica tenemos que:

La serie original (observed) muestra los datos recogidos.
La tendencia muestra los cambios suavizados, como si dibujásemos una línea a través de la mayoría de puntos para mostrar la dirección de la serie.
La estacionalidad captura los ciclos que se repiten mediante un patrón. En esta caso, el eje Y cambia, partiendo de 0 si se mantiene, un valor positivo, si supone un incremento del valor original o negativo si baja su valor. En el gráfico, se puede observar como en un mismo año, las acciones comienzan arriba, para luego bajar y volver a subir.
Si juntásemos la tendencia y la estacionalidad, idealmente, deberíamos obtener la serie original. Pero esto no suele ser la realidad. Los valores residuales a 0 indican que la unión de tendencia y la estacionalidad dan el valor de la serie original. En el resto de casos, corresponde al ruido blanco que no podemos modelar y predecir y que necesitamos para obtener la serie original.

Una serie temporal se dice que es estrictamente estacionaria si sus propiedades estadísticas no se ven afectadas por los cambios a lo largo del tiempo, concretamente:

La media, con su valor promedio permanece constante
La varianza, el ancho de la curva
La covarianza, de manera que la correlación entre puntos es independiente del tiempo

Los procesos estacionarios son más fáciles de analizar, por lo que la mayoría de algoritmos de análisis de series temporales asume que las series son estacionales.

Es decir, que se deberían cumplir tres criterios básicos para poder considerar a una series de tiempo como estacionaria:

https://relopezbriega.github.io/blog/2016/09/26/series-de-tiempo-con-python/

La media de la serie no debe ser una función de tiempo; sino que debe ser constante. La siguiente imagen muestra una serie que cumple con esta condición y otra que no la cumple.
La varianza de la serie no debe ser una función del tiempo. El siguiente gráfico representa una serie cuya varianza no esta afectada por el tiempo (es estacionaria) y otra que no cumple con esa condición.
La covarianza de la serie no debe ser una función del tiempo. En el gráfico de la derecha, se puede observar que la propagación de la serie se va encogiendo a medida que aumenta el tiempo. Por lo tanto, la covarianza no es constante en el tiempo para la serie roja.

Cuando los datos de una serie temporal están distanciados en el tiempo de forma uniforme (por ejemplo, cada semana hay una baja en el consumo de corriente eléctrica en una localidad determinada.) la serie puede asociarse con una frecuencia en pandas.

Tendencias positivas: * Aditivas * Multiplicativas

Tendencias negativas: * Substración * División

Random Walk

A random walk is a sequence where the first difference is not autocorrelated and is a stationary process, meaning that its mean, variance, and autocorrelation are constant over time.

docker run -it -p 10000:8888 -v "${PWD}":/home/jovyan/work --name jupyter-ds jupyter/datascience-notebook

docker run -it -p 10000:8888 -v "C:\Users\Aitor\OneDrive - Conselleria d'Educació\iabd\docs\ts\resources":/home/jovyan/work --name jupyter-ds jupyter/datascience-notebook

https://www.themachinelearners.com/series-temporales-intro/

https://programacionpython.ecyt.unsam.edu.ar/material/08_Fechas_Carpetas_y_Pandas/06_Series_Temporales/ https://medium.com/datos-y-ciencia/modelos-de-series-de-tiempo-en-python-f861a25b9677

Referencias¶

Repositorios GitHub (Timeseries de DataForScience y AdvancedTimeseries de DataForScience) con diversos cuadernos para trabajar con series temporales
Análisis y Predicción de Series de Tiempo - Dr. Lihki Rubio

Proyecto¶

Vamos a realizar un proyecto para predecir el uso de energía mediante la relación entre su consumo y una variedad de factores como la temperatura, la hora, el día de la semana así como otras variables que lleguemos a considerar.

Necesitamos previsiones precisas, ya que hacer previsiones demasiado bajas o demasiado altas tiene sus inconvenientes. La única manera de ganar precisión en las previsiones es entender qué factores influyen en el consumo energético de las personas. Los datos sobre temperatura y energía están probablemente relacionados. Cuanto más calor o frío hace en el exterior, más energía podrían utilizar los edificios de oficinas y los hogares para gestionar la temperatura.

Para este proyecto vamos a utilizar dos datasets, uno con datos de temperaturas por horas (ts_load_metered_20170201_20200131.csv con el campo DATE como fecha) de una estación meteorológica, y otro con el consumo en megavatios (ts_temp_20170201-20200131.csv con el campo datetime_beginning_ept como fecha). Ambos datasets ya se han limpiado para que sólo incluyan un registro por hora.

Los pasos que vamos a realizar son:

Prepara los datos:
1. Carga los conjuntos de datos de energía y temperatura en un único DataFrame uniéndolos por fecha. El resultado sólo debe contener como campos, además de la fecha en formato datetime64, el uso de megavatios por hora (mw de los datos de energía) y la temperatura (HourlyDryBulbTemperature de los datos meteorológicos).
2. Añade nuevas columnas para la hora del día, el día de la semana, el mes y el año de cada registro, y utiliza la fecha como el índice del DataFrame.
3. Revisa si están rellenados todos los datos de temperatura. Si no es así, utiliza la interpolación lineal para fijar estos valores que faltan.
4. Separa el resultado en conjuntos de datos de entrenamiento (hasta nochevieja de 2019) y de prueba (enero de 2020).

Correlación

La correlación mide la fuerza de la relación lineal entre dos variables continuas. Está limitada entre -1 y 1. Los valores cercanos a 0 tienen poca relación entre sí. Los valores cercanos a -1 y 1 tienen relaciones más fuertes. Si la correlación es positiva, también lo es la relación. Cuando una variable aumenta, la otra tiende a aumentar también. Lo contrario ocurre con las correlaciones negativas.

Visualiza los datos para buscar correlaciones:
1. Realiza un gráfico de líneas del consumo de energía y la temperatura a lo largo del tiempo.
2. Obtén la correlación entre el consumo de energía y la temperatura, y argumenta porqué no tiene un valor mayor.
3. Realiza un gráfico de dispersión del consumo de energía frente a la temperatura.